New additions as of OUwie 2.1

It’s been quite a while since we’ve done any active development of OUwie. It was recently brought to our attention that the likelihoods between OUwie and ouch are not the same when the model assumes different OU means (what we refer to here as “OUM”). We would like to thank and credit Clay Cressler for working through our code to identify the specific causes. In doing so, we have taken this opportunity to release a new version of OUwie that provides cleaner output and a number of new capabilities. Some of these new functions were implemented at the request of users, for our own research, and as part of tutorials for various workshops.

Bug fixes and deprecated functions

The differences between OUwie and ouch were traced to two issues. There first being a bug in the most recent version of the weight matrix generation code. For some reason, while looping over the different regimes, the function was not resetting the regime to the regime at the root, and the calculation for the weights for the root regime was missing a $W_{0,i}+e^{(-\alpha_{0,i})}$ term. These are now fixed, and fortunately does not cause any detectable effect on the likelihood, though it does have a slight impact on the estimates of the regime optima.

The second issue is significant and has to do with the way OUwie and ouch construct the variance-covariance matrix when assuming stationarity at the root. In Beaulieu et al. (2012), we expanded upon equation A5 in Butler and King (2004), which assumed that the root optima was estimated. We found that the root regime was hard, if not impossible, to estimate with even moderate values of $\alpha$ (the pull parameter). Because of this, by default we drop the root optima and absorb the weight into whatever regime the root was painted. We incorrectly referred to this as “stationarity”. Ho and Ane (2013) showed that in order to assume true stationarity in an OU model, the covariance requires an additional variance term to account for the fact that, up until $T=0$ , the time at which the clade of interest came into existence, the lineage is assumed to have been evolving in the ancestral regime. For an intuitive example, consider two tips that diverged at the root. Under the original formulation of Butler and King (2004) and Beaulieu et al. (2012) the covariance between the two tips is zero because $s_{ij}=0$ , so $1-e^{-2\alpha s_{ij}}=0$ ). However, with the Ho and Ane (2013) method, an additional $V_{ij} = \frac{\sigma^2}{2\alpha}e^{-2\alpha}$ is added to the variance-covariance matrix.

It is worth pointing out, however, that Ho and Ane (2014a) cautioned that when there are several regimes the stationary distribution does not have a clear definition. This is because it is a weighted average of the regimes the lineage switched between starting from the origin of life to the most recent common ancestor of the focal clade under study. In other words, it’s not as straightforward as integrating over some distribution. For now, OUwie assumes a fixed root, where the $\theta_0$ is equal to whatever regime the root is painted (see below on behavior). In order to make OU1 and OUM models only consistent with ouch we have added the stationarity assumption of Ho and Ane (2014a):

data(tworegime)
pp <- OUwie(tree, trait, model="OUM", root.station=TRUE, scaleHeight=TRUE, shift.point=0, algorithm="invert", quiet=TRUE)

## Warning: The supplied regime painting may be unidentifiable for the regime
## painting. All regimes form connected subtrees.

pp

## 
## Fit
##        lnL      AIC     AICc      BIC model ntax
##  -19.75473 47.50945 48.18742 56.14498   OUM   64
## 
## 
## Rates
##                  1         2
## alpha    1.5935448 1.5935448
## sigma.sq 0.6912515 0.6912515
## 
## Optima
##                  1         2
## estimate 1.6762664 0.3936621
## se       0.1921354 0.3322554
## 
## 
## Half life (another way of reporting alpha)
##         1         2 
## 0.4349719 0.4349719 
## 
## Arrived at a reliable solution

compare this to the new default:

data(tworegime)
pp <- OUwie(tree, trait, model="OUM", root.station=FALSE, scaleHeight=TRUE, shift.point=0, algorithm="invert", quiet=TRUE)

## Warning: The supplied regime painting may be unidentifiable for the regime
## painting. All regimes form connected subtrees.

pp

## 
## Fit
##        lnL      AIC     AICc      BIC model ntax
##  -19.51361 47.02721 47.70518 55.66274   OUM   64
## 
## 
## Rates
##                  1         2
## alpha    1.3916589 1.3916589
## sigma.sq 0.6545502 0.6545502
## 
## Optima
##                  1         2
## estimate 1.6751330 0.2935858
## se       0.1822091 0.3797622
## 
## 
## Half life (another way of reporting alpha)
##         1         2 
## 0.4980726 0.4980726 
## 
## Arrived at a reliable solution

Note that we have also added the new option shift.point into the function call. This allows users to alter the assumption of where the regime shifts occur. By default OUwie() assumes any regime shift occurs halfway down a branch (i.e., shift.point=0.5), whereas ouch assumes a regime shift occurs at the end of the branch (i.e, shift.point=0). Generally speaking, this will have a slight effect on estimates of $\theta_i$ because the position of regime shift point will alter the time spent in each regime.

Finally, we note that we have removed two functions previously available: OUwie.joint() and OUwie.slice(). The OUwie.joint() function was developed for a particular study question (e.g., Leslie et al. 2014), otherwise it is not particularly useful. The function OUwie.slice() was developed and moderately tested, but it does not seem to work particularly well. Both functions are still available by request, and future work will focus on improving and understanding the behavior of OUwie.slice().

New Features

Idenfiability tests

Ho and Ane (2014a) demonstrated that certain regime paintings can produce a ridge in the likelihood surface, which will lead to convergence issues. Specifically, when each regime forms a connected subtree this produces a $m-1$ regime shifts, which is the minimal number. In these situations, the selective optima may not be separately identifiable. In this version of OUwie we have implemented a “identifiability of the regime paintings” check, as both part of the OUwie() function and as a standalone function. With OUwie() by default check.identify=TRUE, and if the check fails, the function will spit out a warning for now. However, this check can be turned off by simply changing check.identify=FALSE. The standalone function simply requires the tree with the regimes painted (either as a simmap object or with node labels) and the data set. Figure 1 depicts a similar example as the one shown in Figure 2 of Ho and Ane (2014a).

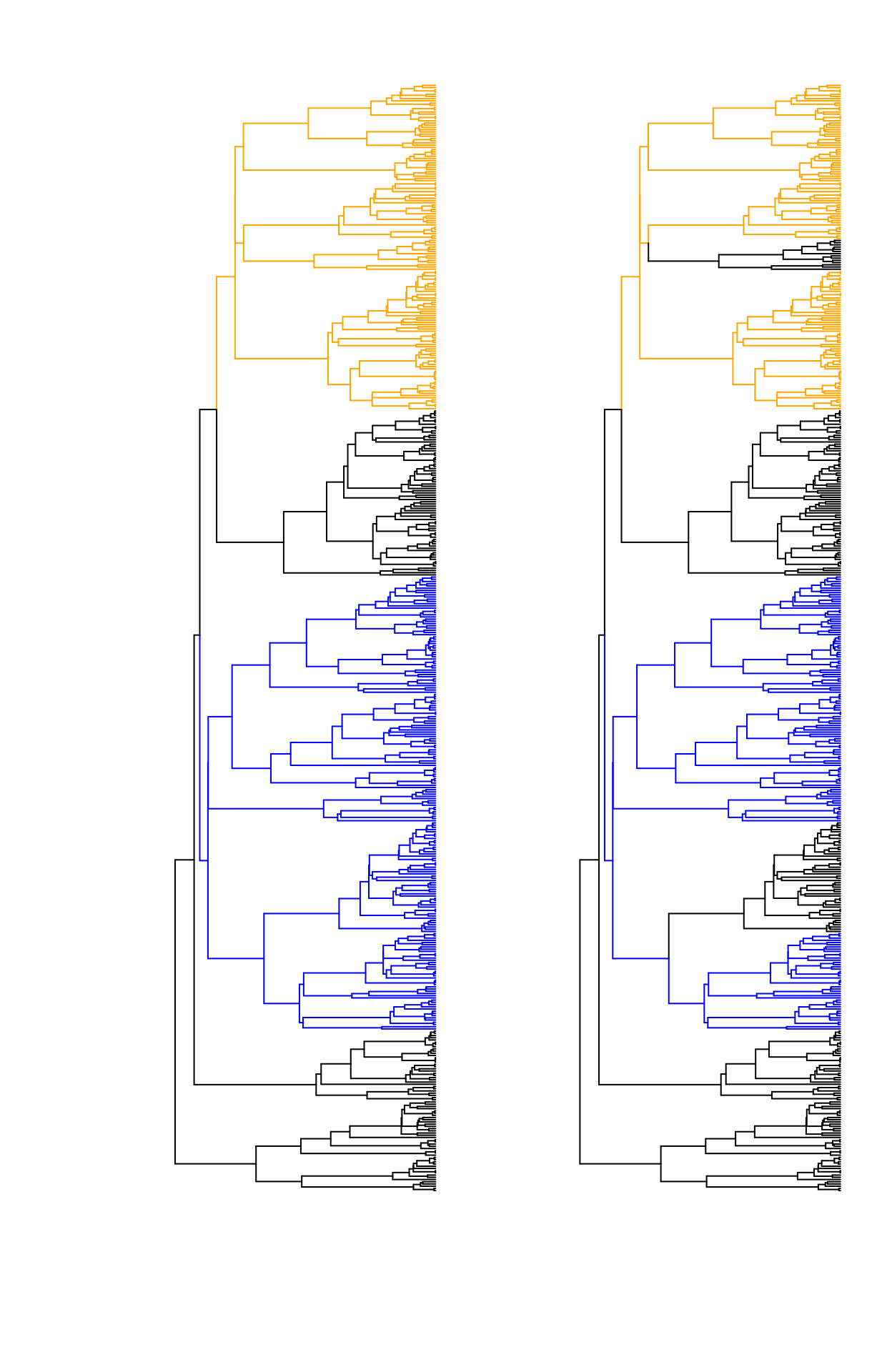
$The edges are painted by regime, assuming an optimum $\theta_i$ for each color. As shown in Ho and Ane (2014a) the left shows an case of unidentifiability case because every regime forms a connected component. The tree on the right shows a case of identifiability because the black regime covers two completely disconnected parts in the tree.$

The edges are painted by regime, assuming an optimum $\theta_i$ for each color. As shown in Ho and Ane (2014a) the left shows an case of unidentifiability case because every regime forms a connected component. The tree on the right shows a case of identifiability because the black regime covers two completely disconnected parts in the tree.

Using the trees in Figure 1, we can conduct a formal test of identifiability of the $\theta_i$ parameters in the model. Let’s try the unidentifiable case:

load("simUnidentifiable.Rsave")
check.identify(phy, data)

## The regime optima are unidentifiable.

## [1] 0

Now, the identifiable case:

load("simIdentifiable.Rsave")
check.identify(phy, data)

## The regime optima are identifiable.

## [1] 1

Another way to diagnose identifiability is to look at the $regime.weights now provided as part of the model fit output. If the weights for every taxon in a given regime are identical, then the expected values of any two taxa in this regime are also identical. This was shown in the mathematical proof of Ho and Ane (2014a, see Appendix 1). It is important to note that we have seen in simulation that even the unidentifiable cases perform well. However, this may be illusory, and we recommend this test always be used as a guide, especially in instances where the resulting model fit is unstable or seems off.

Contour plots

Confidence intervals are typically estimated for each parameter individually. However, the confidence intervals calculated for pairs of correlated parameters can be much wider than their respective univariate confidence intervals. For example, for OU models a decrease in $\sigma^2$ has a similar effect as an increase in $\alpha$ : less variation at the tips. There are differences, of course, so the parameters are identifiable (greater $\alpha$ tends to erase phylogenetic signal, whereas lower $\sigma^2$ does not). For practical problems, it is possible to have a ridge of nearly equal likelihood where if you change just one parameter, this is enough to move it off the ridge, but if you were to change both this would result in simply sliding along the ridge. This “ridge” behavior is precisely what happens when the $\theta_{root}$ is included in the model.

We now allow users to create contour maps of the likelihood surface for any pair of parameters in a given OUwie model. Specifically, we sample a large set of points using a latin hypercube design, and one by one we use these as fixed values for our focal parameters, and we then search for the maximum likelihood estimates for the remaining parameters in the model. This step is done using the new OUwie.contour() function. We will use the trees from above, to show what a “ridge” looks likes.

load("simsOUidentify_8")
surfaceDatThetaR_2 <- OUwie.contour(oum.root, focal.params=c("theta_Root", "theta_2"), focal.params.upper=c(10,10), nreps=1000, n.cores=4)
surfaceDatTheta1_2 <- OUwie.contour(oum.root, focal.params=c("theta_1", "theta_2"), focal.params.upper=c(10,10), nreps=1000, n.cores=4)

We want to look at the likelihood surface for $\theta_{root}$ vs. $\theta_2$ and for $\theta_1$ vs. $\theta_2$ , for an OUM model with the $\theta_{root}$ included in the model. The pair of parameters to examine is passed by focal.param, and the parameters need to be either “theta”, “alpha”, or “sigma.sq”. For example, to look at sigma.sq from the first regime and alpha from the second regime, one would pass focal.param = c( "sigma.sq_1", "alpha_2"). If the regimes are input as characters like, say, flower color, the focal parameter would be focal.param = c( "sigma.sq_Red", "sigma.sq_Blue"). Note that the OUwie.contour function can also be used across multiple processors (n.cores!=NULL). Once the set of points have been evaluated, the plot of the likelihood surface can be generated by inputting OUwie.contour into a plotting function:

plot(surfaceDatThetaR_2, mle.point="red", levels=c(0:20*0.1), xlab=expression(theta[root]), ylab=expression(theta[2]) , xlim=c(0,5,1), ylim=c(0,5,1), col=grey.colors(21, start=0, end=1))

A few notes about the inputs for the plotting function. First, it requires an object of class OUwie.contour. Second, by default mle.point=NULL, which means the MLE point on the surface will not be plotted, unlesss a color is specified. The axis labels can be customized, or left as NULL, in which case the focal.param input from the OUwie.contour function will be used. The limits to both the x and y axes (the first two values), as well as the spacing (the third value) can be also specified. Finally, the levels and the color vector must be of the same length. In the example above, the levels correspond to the space within 2 log-likelihood from the MLE, with colors increasingly becoming lighter as the distance from the MLE increases.

Using a simulated data set, Figure 2 shows the impact of including the $\theta_{root}$ into the model – that is, the likelihood surface forms a ridge where linear combinations of parameter values produce identical likelihoods. In such situations the MLE is undefined and the parameters are generally unidentifiable. When the $\theta_{root}$ is dropped from the model, as shown in Figure 3, MLE estimates of $\theta_{1}$ , $\theta_{2}$ , $\theta_{3}$ are sufficiently peaked and are clearly separately identifiable.

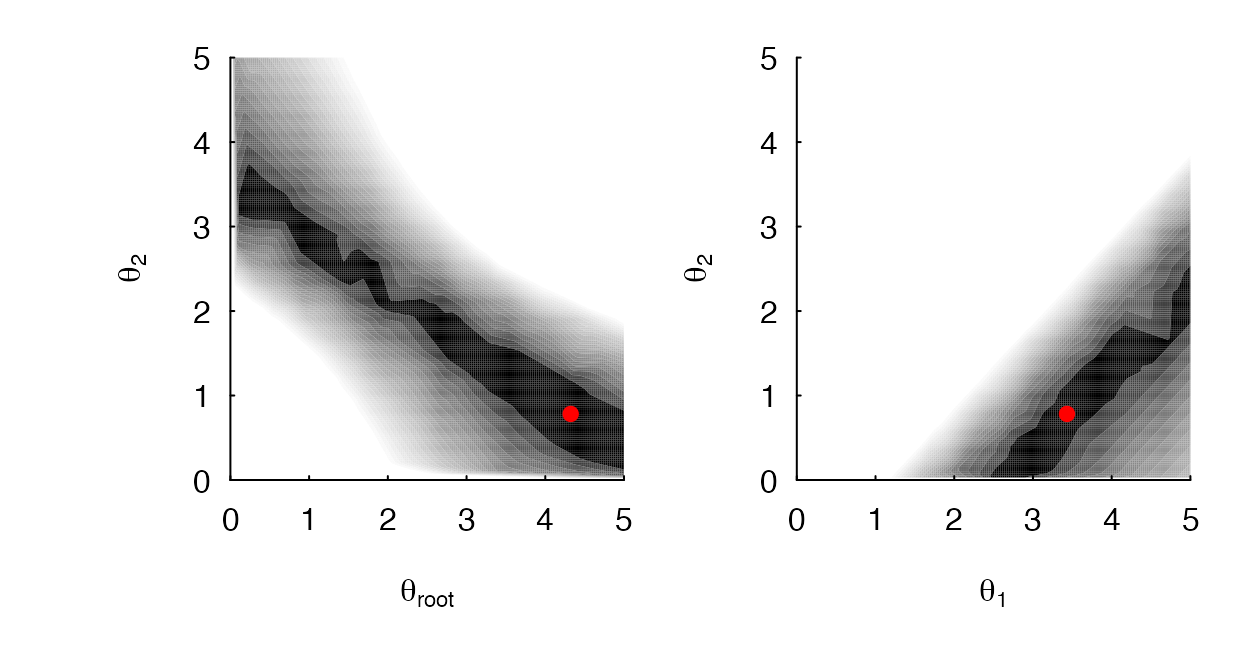
$A contour plot of a OUM model, with the $\theta_{root}$ included in the model. (A) The contour for when $\theta_{root}$ and $\theta_{2}$ are specified as the focal parameters, and (B) shows the likelihood surface for when $\theta_{1}$ and $\theta_{2}$ are specified. In both cases, the likelihood surface appears as a ridge, indicating that the regimes are not separately identifiable.$

A contour plot of a OUM model, with the $\theta_{root}$ included in the model. (A) The contour for when $\theta_{root}$ and $\theta_{2}$ are specified as the focal parameters, and (B) shows the likelihood surface for when $\theta_{1}$ and $\theta_{2}$ are specified. In both cases, the likelihood surface appears as a ridge, indicating that the regimes are not separately identifiable.

$A contour plot of a OUM model, with the $\theta_{root}$ removed from the model. (A) The contour for when $\theta_{1}$ and $\theta_{2}$ are specified as the focal parameters, and (B) for when $\theta_{1}$ and $\theta_{3}$ are specified, the likelihood surface is sufficiently peaked. In other words, the likelihood surface no longer appears as a ridge and regimes are separately identifiable.$

A contour plot of a OUM model, with the $\theta_{root}$ removed from the model. (A) The contour for when $\theta_{1}$ and $\theta_{2}$ are specified as the focal parameters, and (B) for when $\theta_{1}$ and $\theta_{3}$ are specified, the likelihood surface is sufficiently peaked. In other words, the likelihood surface no longer appears as a ridge and regimes are separately identifiable.

Ancestral trait reconstruction

Since OUwie was first released we’ve received a deluge of requests to allow for ancestral trait reconstruction. One such request made its way onto the public R-SIG-PHYLO discussion forum, which stimulated an important conversation about not whether or not you could estimate ancestral states, but, rather, should you. The answer is “it’s complicated” and we honestly don’t recommend it. In our view, the intended use case is just to visualize what the model is saying about evolution to help intuition. For example, is the model something you can believe in? But, if you don’t want to listen to us regarding the merits of ancestral trait reconstructions, here is a sample of comments from other experts in the field:

So in short, yes, you can do it, with any number of methods. But why? If you can answer your biological question with methods that do not involve estimation of a parameter that is inherently fraught with error, it might be better to go another way. Bottom line - use caution and be thoughtful! – Marguerite Butler

I would add an extra caveat to Marguerite’s excellent post: Most researchers work with extant taxa only, ignoring extinction. This causes a massive ascertainment bias, and the character states of the extinct taxa can often be very different to the ancestral state reconstructions, particularly if the evolutionary model is wrong. E.g. there has been an evolutionary trend for example. Ancestral state reconstructions based only on extant taxa should be treated as hypotheses to be tested with fossil data. I wouldn’t rely on them for much more. – Simone Blomberg

While I am at it, let me echo Simone and Marguerite’s warnings. The predicted ancestral states will reflect the process you assumed to predict them. Hence, if you use them to make inferences about evolution, you will recover your own assumptions. I.e. if you predict from a model with no trend, you will find no trend, etc. Many comparative studies are flawed for this reason. – Thomas Hansen

Let me add more warnings to Marguerite and Thomas’s excellent responses. People may be tempted to infer ancestral states and then treat those inferences as data (and also to infer ancestral environments and then treat those inferences as data). In fact, I wonder whether that is not the main use people make of these inferences. But not only are those inferences very noisy, they are correlated with each other. So if you infer the ancestral state for the clade (Old World Monkeys, Apes) and also the ancestral state for the clade (New World Monkeys, (Old World Monkeys, Apes)) the two will typically not only be error-prone, but will also typically be subject to strongly correlated errors. Using them as data for further inferences is very dubious. It is better to figure out what your hypothesis is and then test it on the data from the tips of the tree, without the intermediate step of taking ancestral state inferences as observations. The popular science press in particular demands a fly-on-the-wall account of what happened in evolution, and giving them the ancestral state inferences as if they were known precisely is a mistake. – Joe Felsenstein

The minor twist I would throw in is that it’s difficult to make universal generalizations about the quality of ancestral state estimation. If one is interested in the ancestral state value at node N, it might be reasonably estimated if it is nested high up within the phylogeny, if the rates of change aren’t high, etc. And (local) trends etc might well be reliably inferred. We are pretty confident that the common ancestor of humans and chimps was larger than many deeper primate ancestors, for instance. If N is the root of your available phylogeny, however, you have to be much more cautious. – Nick Matzke

I’ll also add that I think there’s a great deal to be skeptical of ancestral trait reconstruction even when large amounts of fossil data is available. You can try the exercise yourself: simulate pure BM on a non-ultrametric tree with lots of ‘extinct’ tips, and you’ll still find pretty large confidence intervals on the estimates of the trait values. What does it mean to do ancestral trait reconstruction, if our calculations of uncertainty are that broad? – Dave Bapst

These people probably know better than anyone about the power and limitations of the OU model in phylogenetics. So, don’t listen to us, listen to them!

Still determined? Ok, fair enough. It is straightforward to run the ancestral trait reconstruction in OUwie. All you need is an object of class OUwie, which is plugged directly into the new OUwie.anc() function:

data(tworegime)
set.seed(42)
ouwiefit <- OUwie(tree, trait, model="OUM", scaleHeight=TRUE, root.station=FALSE, shift.point=0.5, algorithm="invert", quiet=TRUE, check.identify=FALSE)

recon <- OUwie.anc(ouwiefit)

Ah! If you run the code above a somewhat snarky response is printed to the screen. Since you are here reading this, we think this is sufficient, and you are at least aware that we are not huge fans of this approach. So, there is no need to read the manual (it’s basically the same as what you see here), and the proper way to call the OUwie.anc() function call is simply add in knowledge=TRUE:

recon <- OUwie.anc(ouwiefit, knowledge=TRUE)

## [1] "Doing reconstructions"
## Working on node  1  of  62 Working on node  2  of  62 Working on node  3  of  62 Working on node  4  of  62 Working on node  5  of  62 Working on node  6  of  62 Working on node  7  of  62 Working on node  8  of  62 Working on node  9  of  62 Working on node  10  of  62 Working on node  11  of  62 Working on node  12  of  62 Working on node  13  of  62 Working on node  14  of  62 Working on node  15  of  62 Working on node  16  of  62 Working on node  17  of  62 Working on node  18  of  62 Working on node  19  of  62 Working on node  20  of  62 Working on node  21  of  62 Working on node  22  of  62 Working on node  23  of  62 Working on node  24  of  62 Working on node  25  of  62 Working on node  26  of  62 Working on node  27  of  62 Working on node  28  of  62 Working on node  29  of  62 Working on node  30  of  62 Working on node  31  of  62 Working on node  32  of  62 Working on node  33  of  62 Working on node  34  of  62 Working on node  35  of  62 Working on node  36  of  62 Working on node  37  of  62 Working on node  38  of  62 Working on node  39  of  62 Working on node  40  of  62 Working on node  41  of  62 Working on node  42  of  62 Working on node  43  of  62 Working on node  44  of  62 Working on node  45  of  62 Working on node  46  of  62 Working on node  47  of  62 Working on node  48  of  62 Working on node  49  of  62 Working on node  50  of  62 Working on node  51  of  62 Working on node  52  of  62 Working on node  53  of  62 Working on node  54  of  62 Working on node  55  of  62 Working on node  56  of  62 Working on node  57  of  62 Working on node  58  of  62 Working on node  59  of  62 Working on node  60  of  62 Working on node  61  of  62 Working on node  62  of  62 [1] "Done reconstructions"

From there, you can then easily plot these reconstructions using an internal function that recognizes the OUwie and OUwie.anc class:

A plot of the ancestral state reconstruction under an OUwie model.

Generalized three-point structured algorithm

A long time complaint about OUwie is that it does not scale well when trees exceed 1000 species. This was largely due to the fact that we relied completely on linear algebra functions, in particular, computing the determinant of the variance-covariance matrix, $V$ , as well as inverting it to obtain the log-likelihood and calculate $\theta_i$ . Starting with OUwie version 2.5, we include the generalize three-point algorithm of Ho and Ane (2014b) that bypasses the need for these inefficient calculations. The details of this algorithm are beyond the scope of this vignette and readers should consult Ho and Ane (2014b). The generalized three-point structured algorithm can now be specified in the OUwie() function call:

data(tworegime)
three.point <- OUwie(tree, trait, model="OUMV", root.station=FALSE, scaleHeight=TRUE, shift.point=0.5, algorithm="three.point", quiet=TRUE, check.identify=FALSE)
three.point

## 
## Fit
##        lnL      AIC     AICc      BIC model ntax
##  -14.79505 39.59011 40.62459 50.38453  OUMV   64
## 
## 
## Rates
##                  1        2
## alpha    1.7124628 1.712463
## sigma.sq 0.3518159 1.076873
## 
## Optima
##                 1         2
## estimate 1.676914 0.5567907
## se             NA        NA
## 
## 
## Half life (another way of reporting alpha)
##         1         2 
## 0.4047663 0.4047663 
## 
## Arrived at a reliable solution

We can compare this to the using the standard matrix determinant and matrix inversion:

data(tworegime)
invert <- OUwie(tree, trait, model="OUMV", root.station=FALSE, scaleHeight=TRUE, shift.point=0.5, algorithm="invert", quiet=TRUE)

## Warning: The supplied regime painting may be unidentifiable for the regime
## painting. All regimes form connected subtrees.

invert

## 
## Fit
##        lnL      AIC    AICc      BIC model ntax
##  -14.79506 39.59011 40.6246 50.38453  OUMV   64
## 
## 
## Rates
##                  1        2
## alpha    1.7110818 1.711082
## sigma.sq 0.3517019 1.076479
## 
## Optima
##                 1         2
## estimate 1.676894 0.5563541
## se       0.112031 0.3020699
## 
## 
## Half life (another way of reporting alpha)
##        1        2 
## 0.405093 0.405093 
## 
## Arrived at a reliable solution

In this particular example, the log-likelihoods are identical. However, users are cautioned that some slight differences between the algorithm="invert" and algorithm="three.point" will likely be common. The use of the three-point structured algorithm requires that $\theta_i$ be optimized like any other parameter in the model, whereas with the matrix inversion approach $\theta_i$ are solved numerically. This means that when there are differences in the log-likelihood it is likely because one or more of $\theta_i$ is not at the MLE after using the three-point algorithm. Users are encouraged then to examine the contours of pairs of $\theta_i$ . Also note, that the speed-ups afforded by the three-point algorithm is most observable when the tree size exceeds 500 taxa.

Estimating tip fog

In comparative biology, we often overlook the complexity of uncertainty. We might consider “measurement error” as the standard error of the observed measurements for species, but the common default is to assume this error is zero. Moreover, the array of factors contributing to this uncertainty extends far beyond what we traditionally categorize as measurement error. This intraspecific variance has been described by various terms, including “specific variances”, “residual variation”, “phenotypic variation”, and measurement error. Some of these terms suggest specific mechanisms. Other terms are more descriptive but may have meanings outside the field that can cause confusion. To avoid ambiguity, we recently propose a new term: “tip fog” (Beaulieu and O’Meara, 2024), This term captures the variance that occurs at the present between the true species mean derived from the evolutionary process and what an experimenter records as a value, without being tied to any particular mechanism, and it applies to characters that are discrete or continuous.

There are various ways to specify tip fog. First, recall from the individual manuals that the trait data.frame must have column entries in the following order: species names, current selective regime, and the continuous trait of interest. If the user wants to incorporate tip fog based on their own measurements (tip.fog="known"), then a fourth column must be included that provides the standard error estimates for each species mean. However, a global tip fog for all taxa can be estimated from the data (tip.fog="estimate"). Specifically, to estimate the tip fog parameter:

data(tworegime)
invert <- OUwie(tree, trait, model="OUMV", root.station=FALSE, scaleHeight=TRUE, shift.point=0.5, tip.fog="estimate", algorithm="invert", quiet=TRUE)
invert

In simulation we’ve found that not accounting for tip fog can have a substantial effect on the rate estimates. That is, rates quicky become severally overestimated with even a modest amount of tip fog. It is for these reasons we suggest that user at least set tip.fog="estimate" for now. In future version, this option will become the default.

References

Beaulieu J.M., D.C. Jhwueng, C. Boettiger, and B.C. O’Meara. 2012. Modeling stabilizing selection: Expanding the Ornstein-Uhlenbeck model of adaptive evolution. Evolution, 66:2369-2383.

Butler M.A., A.A. King A.A. 2004. Phylogenetic comparative analysis: A modeling approach for adaptive evolution. American Naturalist, 164:683-695.

Ho, L.S.T., and C. Ane. 2013. Asymptotic theory with hierarchical autocorrelation: Orstein-Uhlenbeck tree models. The Annals of Statistics, 41:957-981.

Ho, L.S.T., and C. Ane. 2014a. Intrinsic inference difficulties for trait evolution with Ornstein-Uhlenbeck models. Methods in Ecology and Evolution, 5: 1133-1146.

Ho, L.S.T., and C. Ane. 2014b. A linear-time algorithm for Gaussian and non-Gaussian trait evolution models. Systematic Biology, 63:397-408.

Jeremy M. Beaulieu and Brian C. O’Meara